Thuật toán BFS – Tìm kiếm theo chiều rộng
1. Mô tả
- Đây là thuật toán tìm các đỉnh bằng cách duyệt theo chiều rộng.
- Xuất phát từ 1 đỉnh và đi tới các đỉnh kề nó, tiếp tục cho đến khi không còn đỉnh nào có thể đi.
- Trong quá trình đi đến đỉnh kề, tiến hành lưu lại đỉnh cha của đỉnh kề để khi đi ngược lại từ đỉnh Kết thúc đến đỉnh Xuất phát, ta có được đường đi ngắn nhất.
- Sở dĩ thuật toán này tìm được đường đi ngắn nhất là nhờ vào cơ chế tô màu và lưu đỉnh cha. Quá trình tô màu khiến 1 đỉnh không thể xét 2 lần trở lên và có thể xem được đường đi từ đỉnh Kết Thúc đến đỉnh Xuất phát dựa vào việc lưu đỉnh cha.
- Sau đây là minh họa về thuật toán:
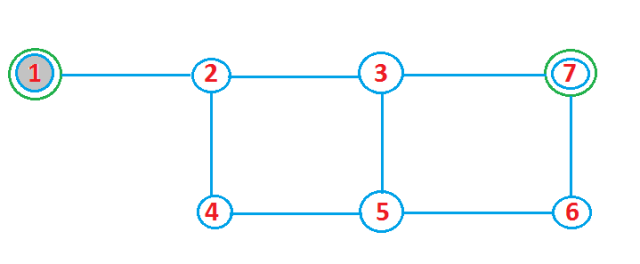
Hình 1
+ Hình 2 : Đi đến đỉnh 2, như vậy nút 1 là nút cha của nút 2
Hình 2
+ Hình 3 : Đã đi hết tất cả các đỉnh kề của đỉnh 1, tiến hành bôi đen đỉnh 1
Hình 3
+ Hình 4: Xuất phát từ đỉnh 2, chọn đỉnh 3, nút cha của đỉnh 3 là đỉnh 2
Hình 4
+ Hình 5 : Xuất phát từ đỉnh 2, bôi đen đỉnh 4, nút cha của đỉnh 4 là đỉnh 2
Hình 5
+ Hình 6 : Đã đi hết tất cả các đỉnh kề của đỉnh 2, tiến hành bôi đen đỉnh 2
Hình 6
+ Hình 7 : Xuất phát tử đỉnh 3, đi đến đỉnh 7, như vậy đỉnh 3 là đỉnh cha của đỉnh 7
Hình 7
+ Hình 8 : Xuất phát từ đỉnh 3, đi đến đỉnh 5, như vậy đỉnh 3 là đỉnh cha của đỉnh 5
Hình 8
+ Hình 3 : Đã đi hết tất cả các đỉnh kề của đỉnh 3, tiến hành bôi đen đỉnh 3
Hình 9
+ Hình 10 : Xuất phát từ đỉnh 5, đi đến đỉnh 6, như vậy đỉnh 5 là đỉnh cha của đỉnh 6
Hình 10
+ Hình 11: Đã đi hết tất cả các đỉnh kề của đỉnh 5, tiến hành bôi đen đỉnh 5
Hình 11
+ Hình 12: Đã đi hết tất cả các đỉnh kề của đỉnh 7, tiến hành bôi đen đỉnh 7
Hình 12
+ Hình 13 : Đã đi hết tất cả các đỉnh kề của đỉnh6, tiến hành bôi đen đỉnh 6
Hình 13
- Như vậy ta vừa đi hết tất cả các đỉnh trong đồ thị, và mỗi lần đi đến đỉnh mới, ta đều lưu lại nút cha của đỉnh mới, dựa vào những đỉnh cha này, ta có liệt kê đường đi ngắn nhất bằng cách đi ngược từ đỉnh Kết thúc, đến đỉnh cha của đỉnh Kết thúc … rồi đến đỉnh cha của đỉnh tiếp theo … đến đỉnh Bắt đầu.
2. Cài đặt
- Hình 14: Cài đặt thuật toán BFS
Hình 14
- Hình 15: In đường đi từ đỉnh Xuất phát đến đỉnh Kết thúc














Không có nhận xét nào:
Đăng nhận xét